Различные формы параллактических звеньев
Рассмотрим различные формы параллактических звеньев.
1. Звено треугольной формы (рис. 1.9, а). По теореме синусов

При v ≈ 90°, sin (φ+v) ≈ cosφ ≈1, sinφ≈; s≈b/φ; lns = lnb-lnφ
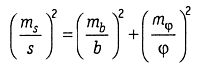
2. Звено с симметричным расположением базиса относительно определяемой стороны (рис. 1.9, б). В прямоугольном треугольнике
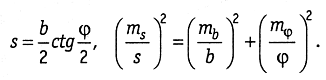
3. Звено ромбической формы с ассиметричным
базисом (рис. 1.9, в). В этом случае
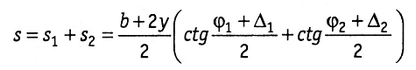
или
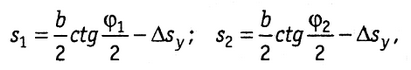
где Δsy = y2/s,y — величина несимметрии базиса. Значение
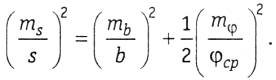
4. Звено ромбической формы с симметричным базисом — частный случай звена ромбической формы с асимметричным базисом, когда у = Δ1 = Δ2 = 0, в этом случае
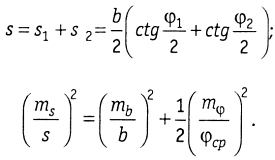
5. Сложное звено треугольной формы (рис. 1.9,
г). По теореме синусов с учетом треугольника с базисом b получаем
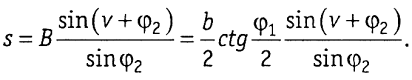
При v = 90°
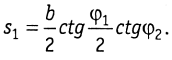
При mφ1 = mφ2 = mφ и mb = 0 имеем
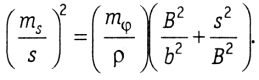
6. Сложное звено, изображенное на рисунке 1.9, д, приводит к формулам
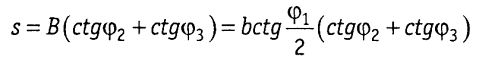
или
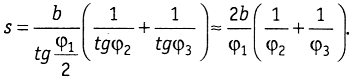
Значение
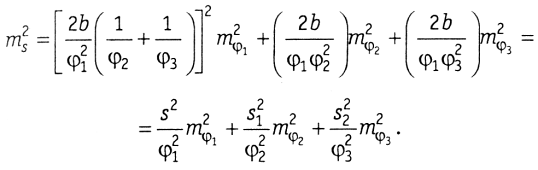
Учитывая s1≈s2≈S/2, находим
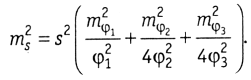
Так как φ1≈ b/B, φ2≈φ3≈2B/S, то при mφ1=mφ имеем
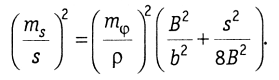
Параллактические углы необходимо измерять с высокой точностью mφ = mβ = 1" теодолитами типа Т2. Для ослабления влияния длинно- и коротко-периодических ошибок делений лимба углы на визирные марки жезла целесообразно измерять на заранее выбранные части лимба, где ошибки в делениях минимальны, на этом же участке лимба нужно измерять параллактические углы и при компарировании жезла на полевом компараторе.

